正态性检验在可以说医学研究中非常重要,也是特别基本的一个统计方法,它可以用来确定数据集是否遵循正态分布。这个假设对于许多统计分析方法来说是基础,如t检验、ANOVA(方差分析)、回归分析等。如果数据不符合正态分布,那么使用这些方法可能会导致误导性的结果。因此,正态性检验是进行这些统计分析前的重要步骤。
适用范围:正态性检验通常用于连续型变量。例如,人体的身高、体重、血压、血糖等可以用来进行正态性检验。如果数据是分类的或者是排名的,那么正态性检验就不适用。
以下是一些常见的正态性检验方法,以及它们之间的一些区别:
数据:演示数据是关于新生儿出生体重影响因素的, 来自R语言自带数据 birthwt
目的:检验bwt是否符合正态性
使用的库:
| 库名 | 用途 |
| pandas | 对数据读取、保存、清洗、转换等 |
| scipy | 对数据进行统计分析 |
| matplotlib | 绘图使用的包 |
数据大致样式:
首先导入库和读取数据:
# 导入库
from scipy import stats
import pandas as pd# 读取数据
df = pd.read_csv("data/birthwt.csv", encoding="utf-8") # 读取数据
print(df.info()) # 打印查看一下数据信息
"""
结果:
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 189 entries, 0 to 188
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 low 189 non-null int64
1 age 189 non-null int64
2 lwt 189 non-null int64
3 race 189 non-null int64
4 smoke 189 non-null int64
5 ptl 189 non-null int64
6 ht 189 non-null int64
7 ui 189 non-null int64
8 ftv 189 non-null int64
9 bwt 189 non-null int64
dtypes: int64(10)
memory usage: 14.9 KB
"""可以看到数据均为 int64 的数值型数据(Python还有string(文本类型数据), 和float(浮点类型数据,也就小数, int是整数类型),数据量为 189,且均没有缺失值
1. **Shapiro-Wilk 测试**:这是最常用的正态性检验方法之一。它的优点是在小样本(例如,n < 50)上有很好的表现,但是在大样本上可能过于保守,即错误地认为数据不符合正态分布。
# 使用stats类的shapiro方法进行正态性检验
shapiro_test = stats.shapiro(df["bwt"])
print(f"Shapiro-Wilk检验: W={shapiro_test.statistic}, p值={shapiro_test.pvalue}")
"""
结果:
Shapiro-Wilk检验: W=0.9924418330192566, p-value=0.43540576100349426
"""结果分析:在进行正态性检验后,P值(或概率值)用于确定数据是否符合正态分布的假设。在这个情况下,P值为0.43540576100349426。通常,如果P值大于0.05,我们就不拒绝原假设,也就是认为数据符合正态分布。反之,如果P值小于0.05,我们就拒绝原假设,认为数据不符合正态分布。在你的情况下,由于P值为0.435,大于0.05,因此我们不拒绝原假设,可以认为数据符合正态分布
2. **Kolmogorov-Smirnov 测试**:这个测试的优点是可以用于任何连续分布的检验,不仅仅是正态分布。但是,对于小样本,它的效力较低。
# 进行Kolmogorov-Smirnov检验
ks_statistic, p_value= stats.kstest(df["bwt"], cdf="norm", args=(np.mean(df["bwt"]), np.std(df["bwt"])))
print('statistic:', ks_statistic)
print('P值:', p_value)
"""
结果:
statistic: 0.04393903797367266
P值: 0.8429042905199977
"""结果显示:P值为0.843,大于0.05,可以进一步的认为bwt符合正态性
3. **QQ图(Quantile-Quantile plot)**:这不是一个形式化的测试,而是一种可视化工具,用于比较观测值和理论分布。如果数据点大致沿着参考线排列,则数据可被认为大致正态分布。
stats.probplot(df["bwt"], dist="norm", plot=plt) # 主要的代码 直接绘制图
plt.title('QQ Plot') # 设置图片标题
plt.show() # 显示图片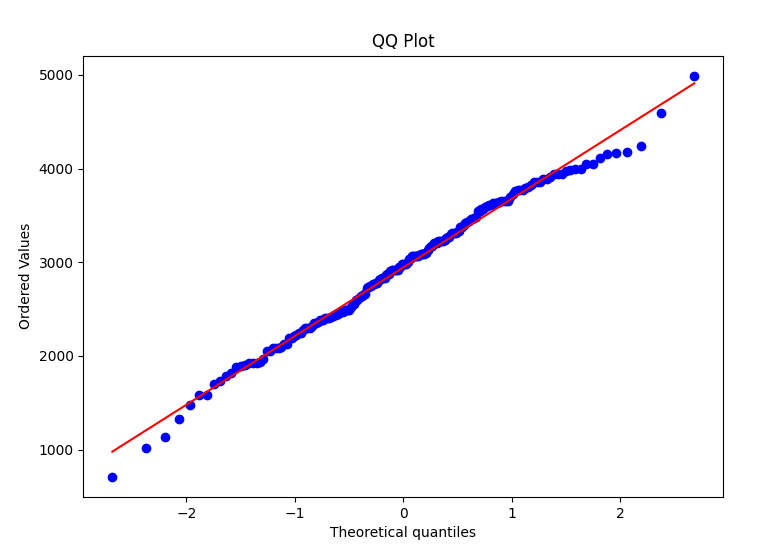
在QQ图中,如果数据点大致沿着一条直线分布,表示样本数据与理论分布(比如正态分布)较好地吻合,可以认为样本数据符合正态分布。如果数据点在较两端出现较大的离散,偏离了直线,表明样本数据不太符合正态分布,可能存在偏态。根据QQ图,可以观察以下几个方面来判断数据是否符合正态分布:
1. 直线的形状:如果数据点大致沿着一条直线排列,即数据点分布在直线周围,且与直线的偏差较小,那么表示样本数据与理论分布的拟合较好,数据可能符合正态分布。
2. 尾部的形状:如果在QQ图的尾部出现较大的离散点,即数据点明显偏离直线,尾部部分呈现曲线或弯曲形状,那么可能表示数据存在偏态。
3. 中央部分的形状:观察数据点在中央区域,特别是在中央部分的集中程度。如果数据点在中央区域较为密集且分布均匀,那么说明数据在中央部分较好地符合正态分布。
4. 离群值:注意是否有明显的离群值,离群值可能会导致数据在QQ图中呈现非线性或曲线状。
需要注意的是,QQ图可以提供初步的判断,但并不能确定样本数据的分布形态。为了更准确地检验数据是否符合正态分布,可以结合其他方法,如统计假设检验或直方图等进一步分析数据的分布特征。
结果:结合图和判断标准,数据基本分布在直线附近,且离群值很少且不是很远,可以大致判断数据为正态
每种方法都有其优点和缺点,选择哪种方法取决于具体的研究问题和数据特性。在进行正态性检验时,重要的是不仅要看测试的p值,还要考虑数据的实际分布(例如,通过绘制直方图或者QQ图)。
