想必大家对I²不陌生,尤其是做患病率Meta分析方面研究的小伙伴们,对于如何正确理解I²值你有把握吗?还在单纯用I²值高低来评估异质性吗?快来一起重新认识I²值!
标题:Meta‐analysis of prevalence: I² statistic and how to deal with heterogeneity
- 患病率的Meta分析:I²统计量以及如何处理异质性
- DOI:https://doi.org/10.1002/jrsm.1547
- 杂志:Research Synthesis Methods
- 影响因子:9.8(Q1)
- 发表时间:2022-1-28
1.有关患病率的系统评价和Meta分析
在过去十年中,回答疾病患病率问题的已发表系统综述(SR)数量增加了十倍。在患病率Meta分析中,点估计代表纳入研究的平均患病率。但是,只有在汇总的不同背景下患病率没有实质性差异时,这种汇总点估计才会提供信息。重要的是“变异性显著” 的定义取决于正在研究的研究问题。对于某些研究问题,即使是少量的变异性也可能被认为是巨大的,而对于另一些研究问题,更大的可变性可能是可以接受的。因此,研究人员在解释疾病患病率的汇总估计值时,必须仔细考虑研究问题和变异来源。
在患病率Meta分析中,估计值的分布,或它们在平均汇总估计值周围的分散程度,与点估计值一样重要。这种分布被称为结果的异质性,它可以提供有关数据变异性的宝贵信息。可以使用各种统计方法来探索异质性,例如I-squared统计量(I²),是用于衡量效应大小中由于非偶然性导致的异质性占总变异的百分比。但是,使用I²并不总是合适的,如果使用不当,可能会得出错误的结论。重要的是要仔细考虑异质性的来源,并在Meta分析中使用适当的统计方法来解释异质性。这在单组率的Meta分析中尤其重要,但也适用于其他类型的数据。
I² 表示观测到的方差中不能归因于抽样误差的比例,并反映了单个研究估计值的置信区间 (CI) 相互重叠的程度。当置信区间存在显著重叠时,I²将较低,这表明研究之间的异质性较低。在重叠最少的地方,I²将很高,这表明研究之间的异质性很高。而CI 是衡量点估计精度的指标,与研究的样本量有关,与异质性没有直接关系。样本量大导致个别研究的置信区间较小,这表明点估计的精度很高。在Meta分析中,置信区间往往不会重叠,从而导致汇总衡量的I²估计值较高,置信区间较宽。
使用任意阈值来定义 I² 的哪个值被归类为高值或低值很常见,但是该统计量并不能直接告诉我们效应的分布或估计值在平均汇总估计值周围的差异有多大,也无法告诉我们估计值的范围是宽还是窄。。因此,高I²估计值不一定是分析中的一个问题,也不是重要的异质性的代名词。同样,I²的低值并不总是表示结果一致和均匀。在解释患病率Meta分析的结果时,必须同时考虑点估计值和估计值的分布,以及研究的临床和方法学异质性。
2.患病率Meta分析中的I²值
作者评估了2017年至2018年间以英文发表并在MEDLINE上编入索引的235份患病率系统综述(SR)的主要特征。其中152篇进行了Meta分析,134篇提及I²。作者纳入了这134篇的初步Meta分析。
值得注意的是这些研究I²的中位数为96.9%(四分位距(IQR)为90.5-98.7)。这意味着Meta分析中包含的研究之间存在高度的异质性。有趣的是,125篇(93.3%)的I²≥ 70%,104篇(77.6%)的I²≥ 90%。这在其他数据类型的Meta分析中并不常见。不同类型研究的系统评价具有不同的I²分布,患病率Meta分析的I²值往往更高。
作者讨论了I²与Meta分析中各种研究变量之间的关系,包括Meta分析中包含的研究数量、合并估计值以及用于数据转换的方法。将I²分为高(> 50%)和低(≤50%)进行分析,这些阈值是在文献中经常使用,尽管没有得到经验证据的支持。需要注意的是这些是事后探索性分析,需要使用其他数据集进行验证。作者还评估了有多少研究进行了灵敏度分析,包括亚组分析、Meta回归和对不同数据转换方法的检验,以及估计的预测区间。
每项Meta分析中包含的研究数量中位数为19,I² > 50%的Meta分析纳入的研究多于I² ≤ 50% 的Meta分析。所有纳入超过19项研究的Meta分析均显示I² > 50%。在极少数情况下在患病率Meta分析中观察到低I²,通常是在研究较少的分析中。作者指出,尽管I²本质上并不依赖于Meta分析中包含的研究数量,但是当纳入的研究数量较低时,I²估计值是有偏差的,有可能偶然观察到较低的I²。
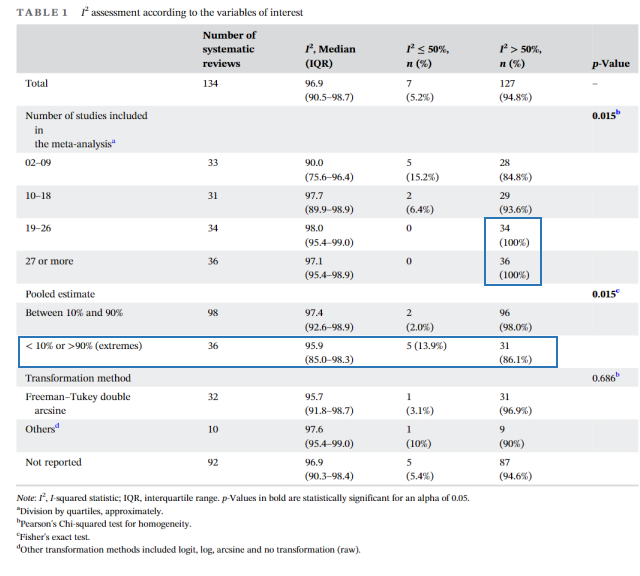
汇总估计值与I²值之间也存在关联。文中提到的表格显示,具有极端汇总估计值(小于10%或大于90%)的Meta分析的I²值往往较低。这意味着,当个别研究的结果非常相似或非常不同时,它们之间的异质性就会降低。
作者没有发现I²的值与用于数据转换的方法之间存在关联,但是,他们指出许多纳入的综述并未报告所使用的转换方法,这可能会限制对结果的解释。
文中还提到,I²值高的研究更有可能进行灵敏度分析。在纳入的综述中只有少数报告了预测区间。这是探索异质性的两种合适的方法。
3.在患病率数据Meta分析中使用I²的思考
衡量Meta分析中异质性的指标I²的估计可能会受到多个变量的影响,例如样本量、方差估计、合并结果类型、单组率Meta分析中使用的转换方法以及结果本身。在评估异质性时考虑这些因素更为重要。
有几个因素可能导致在患病率的Meta分析中经常观察到高I²:
a.首先,患病率自然会因时间、地点和亚组而异,这导致患病率研究存在重要的异质性。
b.纳入样本量大的观察性研究可以得出方差较小的精确估计值,从而产生较高的I²值。
c.非比较单组率Meta数据,例如患病率,通常会导致不同研究之间的分数估计值不同,这导致与相对风险或优势比等比较衡量标准相比,Meta分析的不一致性更大。
举个例子:比如两项样本量均为 200 的假设患病率研究,第一个事件个数为 20(10%),第二个为 40(20%),meta 分析中的汇总测量结果为I² 87%。而对于两项样本量为 200 的比较研究(每组都有 100 名患者),第一个研究事件个数为10 和 20 ,第二个研究分别为 A 组(20)和 B 组 (40),meta 分析结果为RR 0.5,I² 0%。需要注意的是,在这两种情况下,研究2的事件个数都是研究1的两倍,但仅比例meta分析存在不一致。
作者还发现大多数meta分析进行了敏感性分析。但同时作者也指出:如果分析中仅包括少量研究,通常用于探索异质性的亚组分析可能会导致I²值较低。这可能具有误导性,因为它可能表明异质性实际上并不存在。
作者建议使用预测区间代替I²来评估异质性。考虑到数据的不确定性和预期的异质性,预测区间为效应大小提供了一系列预期估计值。这比简单地报告单个I² 值更具信息性,因为它可以让人了解可能的效果大小范围。尽管预测区间具有潜在的优势,但在患病率Meta分析中仍未得到充分利用。
4.在患病率的Meta分析中如何处理实质性和异质性?
患病率的估计值可能因研究的时间和地点以及人群的实际差异等因素而有所不同。这可能会导致真正的异质性,在Meta分析中应始终将纳入和探索这些因素。
I²通常用于评估异质性,但它有局限性,研究者应谨慎解释。较高的I²值不一定代表正在评估的研究问题的相关异质性。强烈建议不使用 I² 的任意阈值。
另外,是否报告Meta分析结果不应仅基于I²来决定。需要注意的是不应根据I²的结果选择用于Meta分析的模型(固定效应或随机效应)。如上文举例所示,仅仅依靠I²来说明异质性可能会产生误导。
I²的置信区间 (CI)、Q 或Tau的平方 也最好是在Meta分析的研究背景下清楚地描述其含义。
作者建议审稿人估计预测区间以探索异质性,但同时检查森林图也很重要,尤其是在研究或异常值很少的情况下。研究应报告汇总估计值的置信区间,但它们可能无法反映结果的异质性。
在具有相关异质性的情况下,合并患病率估计值可能不合适,可以根据先前确定的临床假设进行敏感性分析,例如Meta回归和亚组分析,以避免出现虚假结果。
5.结论
患病率Meta分析中的高I²值很常见,但它们不一定表明研究之间存在重要的差异。需要注意的是,I² 值不是异质性的指标,可能会有偏差。因此,研究者和读者不应过于关注患病率Meta分析中的高I²值。为了评估患病率Meta分析的异质性,预测区间是目前最好的选择。预测间隔提供了一系列值,可用于预测新研究中某种疾病或疾病的患病率。在存在相关异质性的情况下,也建议进行灵敏度分析。
来源:微信公众号 尔云间meta分析,作者 小麦
