主成分（PCA）分析是一种常见的数据降维手段，简单地来说就是原本的数据之间可能存在一定相关性或者数据本身存在不重要的特征，那么我们就可以通过统计学上的方法将原本的相互正交的n维度特征映射到更低维度上如k (k＜n)维上，从而实现降维和聚类。

今天和小伙伴分享一篇使用Prism进行PCA分析的教学文章，内容来自： https://mp.weixin.qq.com/s/GZyLwxTda7DWP56WLCShTA

具体操作流程如下：

1. 新建工程文件，在弹出的向导页面表格类型选Multiple variables，Data table选Start with sample data to follow a tutorial，然后点Create按钮，如下图。

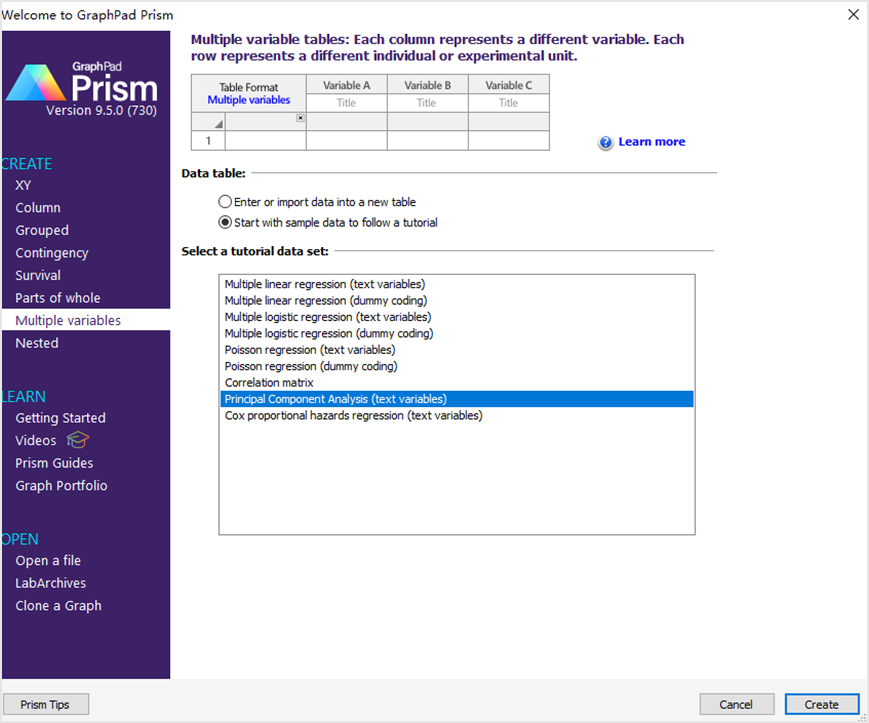
2. 查看数据如下所示。

每张样本图像共记录了 12 个变量，包括 1) 患者 ID 编号；2) 诊断（恶性或良性）；3) 细胞半径；4) 细胞纹理；5) 细胞周长；6) 细胞面积；7) 细胞平滑度；8) 细胞紧凑度；9) 细胞凹陷度；10) 细胞凹点；11)细胞对称性；12) 细胞分形维度。其中，第1和第2列主要是编号和分组信息，我们暂时不用管他们，

3.新建分析，并选择“主成分分析（PCA）”，所处理的数据为所有的数据。

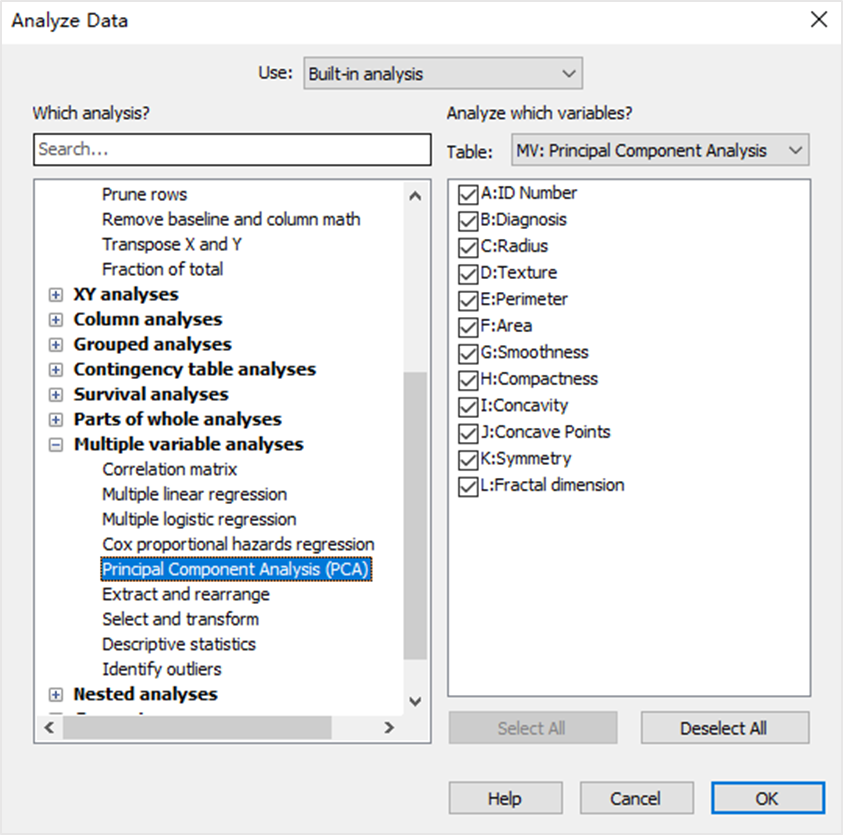
点击OK。进入到如下的界面。

然后我们切换到“Option（选项）中，在分析方法中，我们选择最典型的“select PCs based on eigenvalues (基于特征值选择主成分)，下面其实有很多选择：

1) Select PCs with eigenvalues greater than 1（选择特征值超过1的主成分）

2) Select PCs with eigenvalues greater than X（选择特征值超过X的主成分）

3) Select this many PCs with the largest eigenvalues（选择特征值最大的前X个）

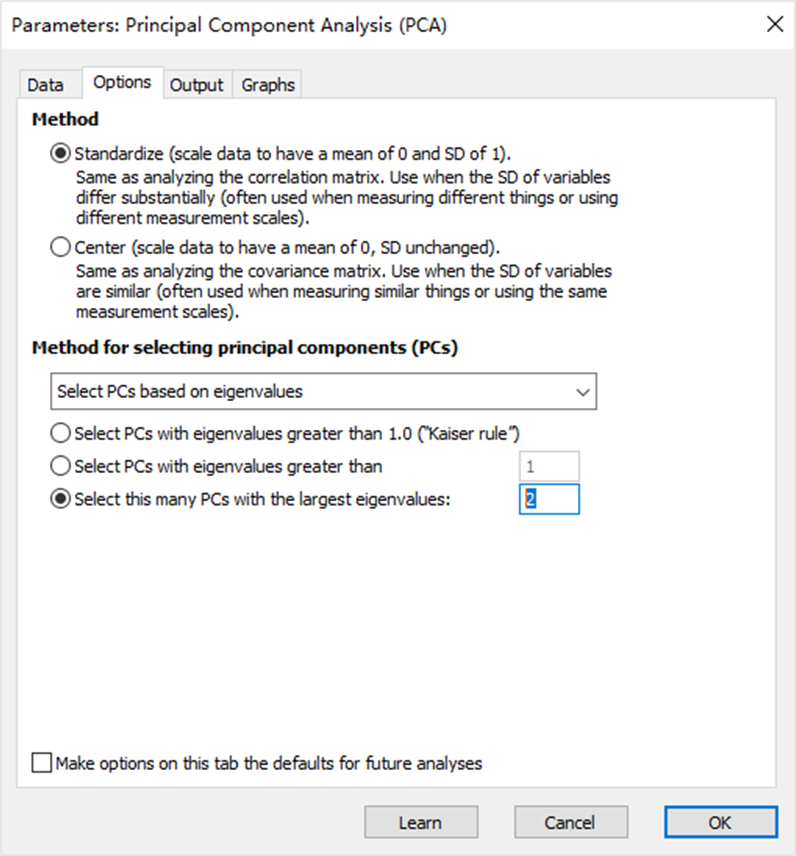
一般来说，选择两个特征值就OK了，因为到了三维Prism就歇菜了。

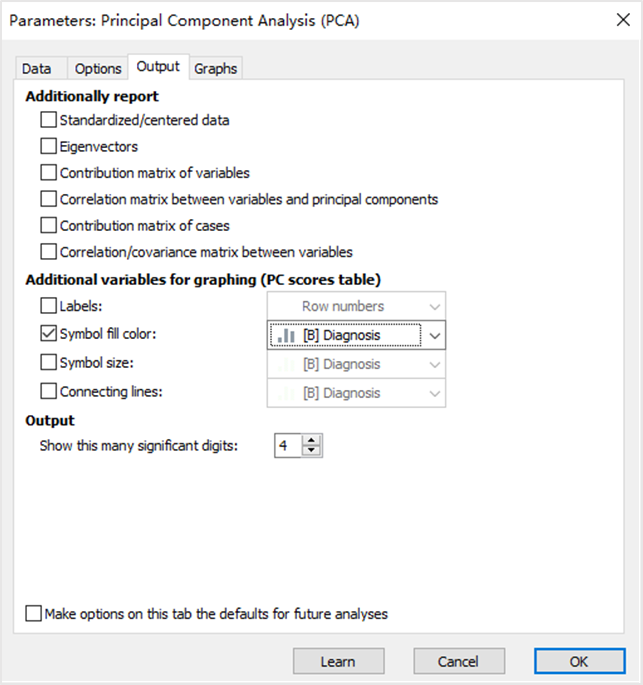
然后，在output里面选择“symbol fill color”，其他的项目我们这里不做过多设置了，

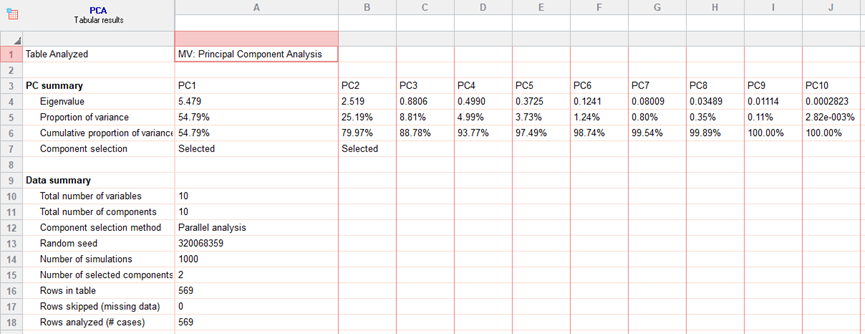
4. 我们可以拿到下面的分析结果，主要关注特征值（Eigenvalue），方差贡献比例（Proportion of variance），和选择的成分的数量(number of selected components)

5. 然后我们进入到“PC scores”绘图界面，并在上方“change”中选择一个配色方案，同时把“legend”进行一下勾选可以得到下图。

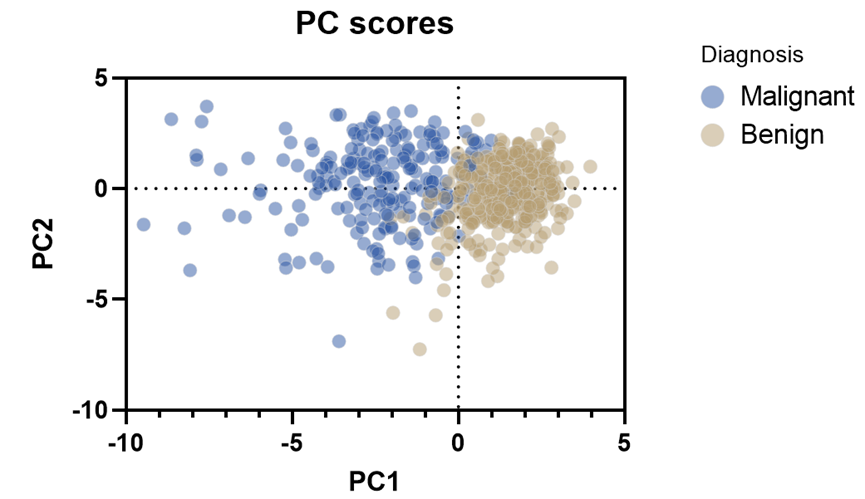
分析：从图中可以看出Malignant数据之间的相似性不太大，因为降维后他的数据整体比较分散。然后对比两者的数据分布，发现两者交叉的地方不多，所以可以说各项因素对Malignant和Benign的影响也是存在差异的。