***本文仅供学习交流***
原著:Matthew L. Maciejewski, PhD; M. Alan Brookhart, PhD
翻译:墨点星沟,医学硕士,公共卫生医师
随机临床试验被认为是医疗干预措施效果最可靠的证据来源,但非实验研究在实际临床实践中也经常被用于评估治疗的有效性。在非实验性研究中,治疗组之间可能因患者的重要特征而不同,如疾病严重程度、虚弱程度、认知功能、对不良反应的易感性和支付能力。1虽然统计调整可以处理组间观察到的特征不平衡,但观察到的不平衡令人担忧,因为它们表明可能存在未观察到的差异。影响治疗和结局的未观察到的患者特征导致的“未观察到的混杂”,是一种不能使用标准统计调整来消除的偏倚。1
当估计非随机研究或有不遵循方案存在的随机研究的治疗效果/处理效应时,工具变量分析可帮助解决未观察的混杂。工具变量是一种可以有效地将一些患者随机分到不同组的因素;它应与所接受的治疗相关,而且仅通过其治疗效果与结局相关。在特定的假设下,即使存在未观察到的混杂,工具变量方法也能提供无偏的治疗效果估计。
在JAMA Network Open上发表的一篇文章中,Desai和他的同事使用工具变量方法评估了2004年至2015年期间因髋部骨折住院的9709名年龄在50岁以上的患者初始使用骨质疏松药物与非椎体骨折风险之间的关联。2作者使用工具变量分析来解决疑似未观察到的混杂,包括虚弱、疾病风险和其他可能导致治疗效果的估计发生偏倚的因素。
方法的应用
为什么使用工具变量?
当患者和临床医生可以自由选择治疗方法时,一些影响治疗选择的因素也可能与良好结局的出现密切相关。在Desai等人2的研究中,男性比女性更不容易开始服用骨质疏松药物,而且他们发生骨折的可能性也更小。如果所有的混杂因素都被观察到,那么潜在的混杂影响可以通过在统计模型中对它们进行调整来解决。如果只观察到一些混杂因素,那么治疗组之间的差异可能是由治疗、混杂因素单独或两者共同造成的。例如,如果骨质疏松症患者因为被认为接近生命的尽头而没有得到预防性治疗,那么没有接受治疗的这组患者可能比接受治疗的患者病情更严重或更虚弱。如果本研究中未测量的衰弱影响了患者的预后,并且在组间不平衡,那么衰弱将是一个未测量的混杂因素,并将在回归或倾向评分方法中使得治疗效果的估计产生偏倚。3在评估治疗(髋骨骨折后骨质疏松治疗的开始)和预后(预防随后的非椎体骨折)之间的关联时,与治疗密切相关的工具变量可以用来帮助减少未观察到的混杂的影响。在Desai等人的报告中,考虑到的4个工具变量中最优的是基于髋骨骨折后医院层面的骨质疏松药物处方率。因为一些医院的医生会常规开展骨质疏松治疗,一些医院的医生则不会。
什么是工具变量?
工具变量类似于随机化过程,可以有效地将一个子集的患者随机分配到不同的治疗组,以实现观察到的和未观察到的因素的平衡分配 (见补充材料中的附表,以往研究中使用的工具变量清单),而对结果没有任何直接影响。举个例子4,每周的入院日是评估医疗费用与2种肾结石取出方法 (内科和外科) 之间关系的工具变量。入院日与干预类型相关,因为手术治疗更可能在工作日而不是周末进行。因此,该工具变量-入院日-可能近似于临床试验中的随机化过程。因紧急原因入院的患者 (如急性肾绞痛),一周内的日子可以近似随机化程序,但因选择性原因入院的患者(如整形手术)则不能。
如果入院日期不太可能与感兴趣结局的变化相关,除了与是否提供诊疗或手术干预的潜在关系外,那么该变量可能是一个合适的工具变量。当研究者确定了一个看似有效且可测量的工具变量后,就可以进行工具变量分析。尽管有许多不同的方法,工具变量分析通常是使用一个两阶段回归模型。在第一阶段,建立估计接受某种治疗概率的模型,这取决于工具变量和其他患者因素。根据这个概率模型,预测每个患者的治疗概率,以及实际接受治疗与预测治疗之间的差异 (称为“残差”)。在第二阶段,将预测的治疗概率5或残差6与患者因素一起纳入到一个传统的回归模型中进行估计,该回归模型的因变量为结局指标。
工具变量估计的局限性
尽管工具变量可以在存在不可测量的混杂因素时提供因果关联的估计,但这些分析很难实现和解释。第一个挑战是找到一个貌似可以预测治疗,但又对结局无直接或间接影响的变量。为了评估工具变量分析的执行和结果报告1, 7,应该提供强有力的理由来解释为什么传统方法可能导致未观察到的混杂,为什么选择的工具变量可能被期望与治疗分配密切相关,以及为什么工具变量应该仅通过其对治疗的影响与结果相关。在预测治疗的第一阶段模型中,这些理论论证应该得到与治疗密切相关的经验证据的支持。
第二个挑战是关键的工具变量假设,即工具仅通过其对治疗的影响与结果相关,无法用数据证实。要检验是否没有从工具变量到结局的独立因果路径,需要控制所有混杂因素。然而,激发工具变量分析需要的未观察到的混杂,排除了对这一假设的检验。如果所有的混杂因素都被观察到,就没有必要进行工具变量分析。如果工具变量能有效地随机化患者,那么它应该与观察到的患者特征无关。涉及工具变量分析的报告通常包括一个表,其中总结了工具变量各水平的观察到的患者特征的均值和频率。该工具仍有可能与未观察到的变量有关,因此研究人员应该提出一个强有力的论点,说明为什么这种可能性不大 (见补充材料)。
第三个挑战是工具变量方法估计的治疗效果/处理效益往往难以解释。在特定的假设下5,工具变量估计只适用于治疗状态依赖于工具变量的患者,即已进入“依从者”或“边缘患者”的亚组。5, 7如果治疗以类似的方式影响所有患者,则工具变量分析的估计应推广到所有患者。描述工具变量分析结果的报告应讨论治疗效果估计的解释,包括边缘患者的特征描述。
第四个挑战是当一个工具变量与治疗弱相关时,这个问题可能会导致较宽的置信区间 (CI) 的估计偏倚。7, 8弱工具变量只与少数患者的治疗相关,因此有效地减少了样本量。8如果工具变量很强,并且基本假设成立,那么工具变量方法可能在强烈怀疑存在未观察到的混杂的情况下有用。
工具变量是如何使用的?
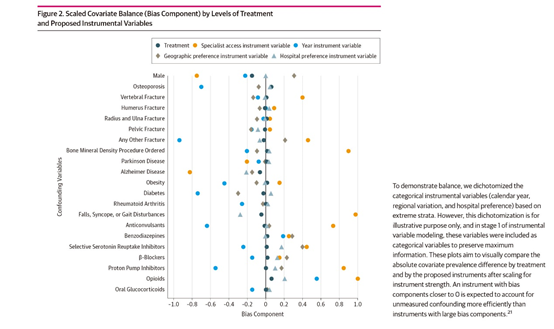
Desai等人2的研究考虑了4个工具变量:日历年、专家可及性、不同地域的骨质疏松药物处方率和医院偏好。这些工具变量尝试利用日历时间、医生、地理区域和医院的治疗选择的随机方差。作者发现,在比较接受骨质疏松药物治疗的患者和未接受药物治疗的患者时,一些患者的协变量是不平衡的,但在比较患者的骨质疏松药物处方率的医院特异性差异时,不平衡的程度较轻 (见Desai等人2文章的图2)。作者检查了工具的性能,发现医院特有的处方措施是解决未观察到的混杂的最合适的措施,因为它与治疗最密切相关。Desai等人也进行了常规回归分析,与工具变量估计的结果进行比较。
工具变量分析应如何解释呢?
作者得出了两个结论。第一,骨质疏松症药物治疗可能与近期髋关节骨折的成人非椎体骨折风险降低有关。这一结果可能并不适用于所有符合接受骨质疏松药物治疗的患者,因为该队列相比之前研究中的医保队列较年轻,共病较少。第二,未观察到的混杂可能导致骨质疏松药物治疗与非椎体骨折之间关联的低估 (在多变量调整分析中,发病密度的差异为1.3/100人年;而在工具变量分析中,发病密度差异为4.2/100人年)。
参考文献
1. BrookhartMA, Rassen JA, Schneeweiss S. Instrumental variable methods in comparative safety and effectiveness research. Pharmacoepidemiol Drug Saf. 2010;19(6):537-554.
2. Desai RJ, Mahesri M, Abdia Y, et al. Association of osteoporosis medication use after hip fracture with prevention of subsequent nonvertebral fractures: an instrumental variable analysis. JAMA Netw Open. 2018;1(3):e180826.
3. Haukoos JS, Lewis RJ. The propensity score. JAMA. 2015;314(15):1637-1638.
4. Hollingsworth JM, Norton EC, Kaufman SR, Smith RM,Wolf JS Jr, Hollenbeck BK. Medical expulsive therapy versus early endoscopic stone removal for acute renal colic: an instrumental variable analysis. J Urol. 2013;190(3):882-887.
5. Angrist JD, Imbens GW, Rubin DB. Identification of causal effects using instrumental variables. J Am Stat Assoc. 1996;91(434):444-472.
6. Terza JV, Basu A, Rathouz PJ. Two-stage residual inclusion estimation: addressing endogeneity in health econometric modeling. J Health Econ. 2008; 27(3):531-543. doi:10.1016/j.jhealeco.2007.09.009
7. Ertefaie A, Small DS, Flory JH, Hennessy S. A tutorial on the use of instrumental variables in pharmacoepidemiology. Pharmacoepidemiol Drug Saf. 2017;26(4):357-367. doi:10.1002/pds.4158
8. Hernán MA, Robins JM. Instruments for causal inference: an epidemiologist’s dream? Epidemiology. 2006;17(4):360-372. doi:10.1097/01.ede.0000222409.00878.37
