上次我们介绍了观察性疗效比较研究中已测量混杂因素的统计学分析方法(如何控制观察性疗效比较研究中的混杂因素:(一)已测量混杂因素的统计学分析方法 ),那对于未知或未测量混杂因素的统计学分析方法该怎么选择呢?
人们对事物的认识是一个逐步修正、不断完善的过程。目前,对复杂疾病尚未找到所有的混杂因素,未知的混杂因素,或虽已知但实际测量有困难的混杂因素是观察性疗效比较研究(CER)中的重大挑战,也是混杂因素控制方法学研究的焦点。针对未知或未测量的混杂,本文从统计学角度就设计良好的观察性CER中如何进行混杂因素的统计分析进行述评,并对其正确应用进行总结。本文中将未知混杂和已知但未测量混杂统称为未测量混杂(unmeasured confounder)。
1.未测量混杂因素的常用控制方法
根据文献综述,近年来观察性研究中最常用的分析方法有3类,包括工具变量法(instrumental variable),其次双重差分模型(difference-in-differences,DiD),本底事件率比校正法(prior event rate ratio adjustment,PERR),及其衍生方法。
(1)工具变量法:是由PG. Wright于1928年首次提出,最早应用于经济和社会学,最近开始用于流行病学领域对未测量混杂因素的控制。工具变量需满足:与所研究的干预相关;与结局无关,仅通过干预因素影响结局;独立于混杂因素。见图 1。
图1 工具变量
工具变量法的统计原理:假设Y为结局,G为协变量,在传统最小二乘法统计模型的左右两边增加工具变量Z,同时取协方差,可得:
工具变量法的作用和随机分组异曲同工,随机分组与所有混杂因素无关,与实际接受的治疗相关,只有通过治疗影响结局,因而事实上,随机分组变量就是一个工具变量。Brookhart等使用此法分析了非选择性Cox-2抑制剂、非载体抗炎药与胃肠道并发症的关联,选择医生的处方习惯作为工具变量,分析结果与另外两个临床试验结果类似,但如采用传统的多元回归进行协变量调整,结果却相反。



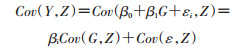










确认删除