作者:张耀文
1、问题与数据
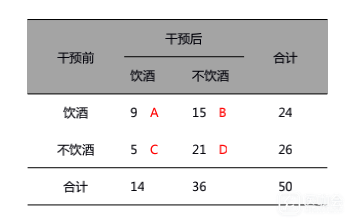
某研究者想要观察戒酒干预的效果,招募了50例研究对象,其中饮酒者24例,不饮酒者26例,饮酒率为48%。所有研究对象均观看饮酒造成严重交通事故的视频。两周后,研究者询问研究对象的饮酒状态,其中饮酒者14例,不饮酒者36例,饮酒率为28%。
看起来戒酒干预是有效的,饮酒率从48%下降到28%,但是这个下降是否有统计学意义呢?
2、McNemar’s检验
McNemar's检验(配对卡方检验)用于分析两个相关率的变化是否有统计学意义。
首先,需要将数据整理成2*2的四格表(如单元格A表示干预前和干预后都饮酒的9人)。
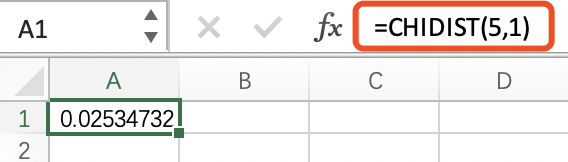
McNemar’s检验的公式χ2 = (B-C)2/(B+C),对于上述数据χ2 = (15-5)2/(15+5)=5.000,根据自由度为1的卡方分布,可利用EXCEL根据该卡方值计算对应的P值=0.025。
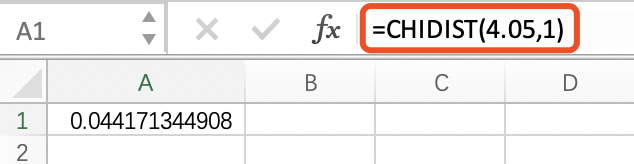
北京大学医学出版社2006年出版的《卫生统计学教程》中写到,当B+C≤40时,还需要做连续性校正,χ2 = ( |B-C| -1)2/(B+C),则上述数据对应的χ2 = ( |15-5| -1)2/(15+5)=4.050, 该卡方值对应的P值=0.044。
3、SPSS计算
McNemar’s通过SPSS计算的详细步骤可见(SPSS详细操作:配对卡方检验(McNemar’s test)),上述数据得到的结果是:
可以看到SPSS给出了Asymptotic Sig. (2-sided test),该行的值是经过连续校正后的P值。而Exact Sig. (2-sided test) 是根据二项分布计算精确P值。SPSS中,非对角线格子(B+C)的观测数大于25时,不展示精确P值,只展示近似P值。
















确认删除