一、问题与数据
最大携氧能力(maximal aerobic capacity,VO2 max)是评价人体健康的关键指标,但测量方法复杂,不易实现。具体原因在于,它不仅需要昂贵的试验设备,还需要研究对象运动到个人承受能力的极限,无法测量那些没有运动意愿或患有高危疾病无法运动的研究对象。因此,某研究者拟通过一些方便、易得的指标建立研究对象最大携氧能力的预测模型。
该研究者已知研究对象的年龄和性别与最大携氧能力有关,但这种关联强度并不足以建立回归模型,预测最大携氧能力。因此,该研究者拟逐个增加体重(第3个变量)和运动后心率(第4个变量)两个变量,并判断是否可以增强模型的预测能力。
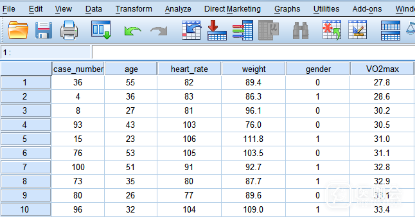
研究者共招募100位研究对象,分别测量他们的最大携氧能力(VO2 max),并收集年龄(age)、性别(gender)、体重(weight)和运动后心率(heart_rate)变量信息。部分数据图1。
图1 部分数据
二、对问题分析
研究者已知某些自变量(age和gender)与因变量(VO2 max)有关,拟判断逐个增加自变量(weight和heart_rate)后对因变量预测模型的改变。针对这种情况,我们可以使用分层回归分析,但需要先满足以下8项假设:
假设1:因变量是连续变量。
假设2:自变量不少于2个(连续变量或分类变量都可以)。
假设3:各观测值之间相互独立,即残差之间不存在自相关。
假设4:因变量和自变量之间存在线性关系。
假设5:残差的方差齐。
假设6:不存在多重共线性。
假设7:没有显著异常值。
假设8:残差近似正态分布。
假设1和假设2与研究设计有关。本研究数据符合假设1和2。如何考虑假设3-8呢?

















确认删除