一、问题与数据
某研究者猜测,45岁至65岁健康男性中,久坐时间较长者,血液中的胆固醇浓度要高一些。因此拟开展一项研究探讨胆固醇浓度与久坐时间是否有关,并希望通过久坐时间预测胆固醇浓度。研究者收集了研究对象每天久坐时间(变量time)和胆固醇浓度(变量cholesterol)。部分数据如图1。
图1 部分数据
二、对问题分析
研究者想判断两个变量之间的关系,同时用其中一个变量(久坐时间)预测另一个变量(胆固醇浓度),计算其中一个变量(久坐时间)对另一个变量(胆固醇浓度)变异的解释程度。针对这种情况,可以使用简单线性回归分析,但需要考虑7个假设。
假设1:因变量是连续变量。
假设2:自变量可以被定义为连续变量。
假设3:因变量和自变量之间存在线性关系。
假设4:各观测值之间相互独立,即残差之间不存在自相关。
假设5:因变量没有显著异常值。
假设6:残差的方差齐。
假设7:残差近似正态分布。
假设1和假设2与研究设计有关。经分析,本研究数据符合假设1和2。如何考虑和处理假设3-7呢?
三、SPSS操作
3.1 检验假设3:因变量和自变量之间存在线性关系
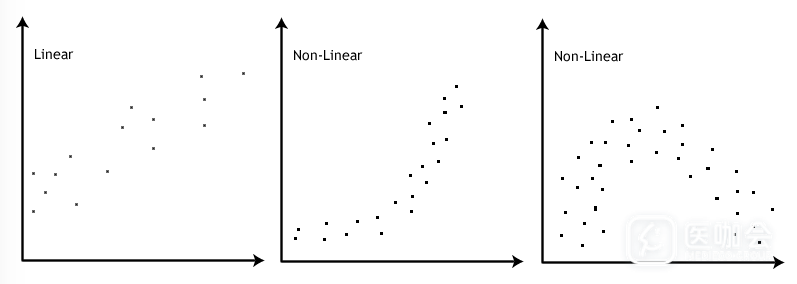
简单线性回归要求两个变量之间存在线性关系。本例要求观久坐时间(time)和胆固醇浓度(cholesterol)之间存在线性关系。要确定是否存在线性关系,研究者需要查看两个变量的散点图。如果散点图大致呈一条直线,说明有线性关系。但是,如果不是一条直线(如一条曲线)则没有线性关系。散点图2给出了线性和非线性关系的例子。
图2 两个变量的散点图
这样的散点图用SPSS怎么画呢?
在主界面点击Graphs→Chart Builder,在Chart Builder对话框下,选择Gallery→Choose from→Scatter/Dot。选择Scatter/Dot后,在中下部呈现8种图形。选择 “Simple Scatter”,并拖拽到主对话框中。如图3。

















确认删除